Quantum Cryptography
Quantum Cryptography depends on physics instead of math, like classic cryptography. A truly random cryptographic key is generated and used for encryption only once (One Time Pad), guaranteeing the encrypted data to be secure – today and forever Any attempt to intercept the exchange of the key causes detectable variations in the quantum states carrying the cryptographic key, alerting both sender and receiver to the attack and allowing them to take mitigating action. The key is absolutely secure, as the one-time-pad key delivery is no longer dependent on human couriers.
First Generation QKD is based on “single photon” technology, which requires complex and expensive equipment to generate and detect single photons (particles) of light. A key is transmitted using single photons. This transmission is untappable as any attempt at eavesdropping results in detectable variations in the quantum states of the photons, thereby revealing the eavesdropper. There are many disadvantages of QKD such as:
1. The need for single photon emitters as well as detectors capable of counting these photons arriving at the destination. Such equipment is highly specialized and expensive, with costs in the order of tens of thousands dollars apiece.
2. These systems are also delicate as they employ highly sensitive equipment, which can be costly to maintain. In fact, the detectors used are so sensitive that even in a dark room, opening them up would saturate the sensors and destroy the device.
3. The responsiveness of this type of system is slow, yielding secret key rates typically below 100kbps. Given the volumes of data transmitted over information networks today, such key generation rates are usually insufficient to allow true OTP encryption. As a result, first generation QKD technology is generally used in a hybrid configuration – in conjunction with classical encryption – to provide enhanced security, but does not yield a truly future-proof system.
To explain QKD, a theoretical situation will be used to explain the process of using QKD.
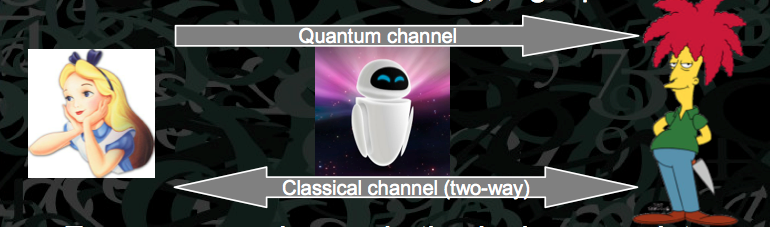
There are two 'people', Alice and Bob who are trying to comunicate with each other. Alice and Bob both have access to a quantum channel and a classical channel. Eve, is an eveasdropper, and has unlimited computational power, and must simply obey the laws of physics.
1. Alice generates a random bit, "0" or "1", with equal probability to encode.
2. Alice chooses at random one of two bases (Horizontal/Vertical or anti-diagnal/diagnal, typically) in which to encode her bit.
3. Alice entangles a pair of photons, and sends one of the photons, prepared in the appropriate polarisation state, to Bob, and notes the basis and bit value sent.
4. Eve has the option to eveasdrop. Eve chooses at random in which basis to measure, and makes a measurement on the photon recieved She then proceeds to entangle another pair of photons with the same bases and measurement as she measured, and send one of the entangled photons to Bob. Eve now may have access to some of the key Alice sent to Bob.
Explaination: If Eve and Alice both measure in the same bases, in a idealistic situation, Eve will get the same value as Alice. This means Eve has successfully eveasdropped, as Bob recieved the same type of qubit as Alice sent. If Eve measures in the other bases, she has a 50% probability of getting the same value as Alice, as the value of the other bases is a superposition of the bases. If Eve measures in the wrong basis, the wrong qubit may be sent to Bob, resulting in variation in the raw key between Alice and Bob.
5. Bob chooses at random in which basis to measure, and makes a measurement on the photon recieved, making note of the value and bases measured in. The resulting string of bits is the raw key.
Explaination: If Bob and Alice both measure in the same bases, in a idealistic situation, Bob will get the same value as Alice. If Bob measures in the other bases, he has a 50% probability of getting the same value as Alice, as the value of the other bases is a superposition of the bases.
6. Through the classical channel, Bob and Alice share what bases they measured in. Both parties will disregard any measurements made when the bases do not agree.
7. To check whether Eve has eveasdroped, Alice and Bob will announce a small section of their bits over the classical channel to see for variation. All variation is assumed to be a result of Eve. The small section of bits will be discarded.
